Geometry
Seminar
Variational formulas for Robin’s constants on pseudoconvex
domains
(à la Yamaguchi)
Mr. Shu-Fai Chan
Department
of Mathematics, The University of Hong Kong
Abstract
Let D
be an unramified covering domain over an open set in ![]() ,
, ![]() , with smooth boundary. For each fixed point
, with smooth boundary. For each fixed point ![]() in D, let
in D, let ![]() be Green's function on D
with the pole at
be Green's function on D
with the pole at ![]() with respect to
the Euclidean metric. The Robin constant at the point
with respect to
the Euclidean metric. The Robin constant at the point ![]() is defined as
is defined as
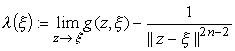
When D is a smoothly
bounded pseudoconvex domain over ![]() , Hiroshi Yamaguchi proved that both
, Hiroshi Yamaguchi proved that both ![]() and
and ![]() are real-analytic
strictly plurisubharmonic exhaustion functions
on D.
are real-analytic
strictly plurisubharmonic exhaustion functions
on D.
Yamaguchi's method is to
study variations of domains![]() . By using a variational formula
for
. By using a variational formula
for ![]() in terms of the
boundary behavior of Green's function, he was able to apply boundary condition
of certain type of pseudoconvex domain with smooth
boundary and proved that
in terms of the
boundary behavior of Green's function, he was able to apply boundary condition
of certain type of pseudoconvex domain with smooth
boundary and proved that ![]() is superharmonic. This result was then applied to get the main
theorem, where the total space is only assumed to be pseudoconvex.
In this talk, we shall examine his method in detail.
is superharmonic. This result was then applied to get the main
theorem, where the total space is only assumed to be pseudoconvex.
In this talk, we shall examine his method in detail.
|
Date: |
November 3, 2005 (Thursday) |
|
Time: |
4:00 – 5:00pm |
|
Place: |
Room 517, Meng Wah Complex |
|
|
All are welcome |
|